Heat transfer
Heat transfer is a very complicated process involving many parameters and conditions. This page plays the role of introduction to heat transfer and a documentation on the methods used to calculate the heat transfers applied to our vehicle.
Heat transfers
A heat transfer is basically an energy transfer that can produce work or a change of temperature difference between the interacting parts. It can take three forms: conductive, convective and radiative. In the case of a heat transfer due to the atmosphere around an aircraft, the three mechanisms are effective. This page currently focuses on convective heat transfer, which implies conductive heat transfer. Radiative transfer is probably negligible before the two others in our particular case study.
Introduction to heat convection and conduction
Heat convection occurs when there is a fluid flowing around a control volume at a temperature different than the control volume's. The flow can be either natural, when the fluid is flowing due to density gradients (buoyancy force), or forced, when the fluid is flowing because an external process force it to flow or make the control volume move through the fluid.
When air is the considered fluid, convection is always associated to conduction heat transfer. The reason is that a film is formed on the surface of the object, called the boundary layer, and it is partly steady and at a temperature closer than the temperature of the object than the temperature of the fluid. In that case, conduction applies.
An insulation layer's effect can be easily calculated as its thermal transmittance (U-value) or resistance (R-value), the amount of heat that it allows to be transferred through it. This is directly obtained from the material's thermal conductivity k (unit: W/m.K) and the thickness of the insulation L. R = L/k and U = k/L. Unit of U is W/m^2.K. The transmitter heat is then Φ = A × U × (T1 - T2), in Watt (= Joule/s), where A is the external area of the insulation layer, T1 and T2 are the internal and external temperature. Examples for the transmittance of insulation layers can be found here [1],
Heat transfer coefficient h
The rate of heat loss of a body by convection is proportional to the difference in temperatures between the body and its surroundings, as stated by Newton's law of cooling: 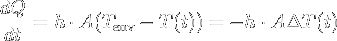 , where h is the heat transfer coefficient. This h depends on many parameters (flow rate, surface roughness, fluid properties, and others) and is very hard to calculate accurately. Approximations exist for some conditions and determining them is still an active research topic for some conditions. It will be our main problem in the case of air to aircraft heat transfer.
, where h is the heat transfer coefficient. This h depends on many parameters (flow rate, surface roughness, fluid properties, and others) and is very hard to calculate accurately. Approximations exist for some conditions and determining them is still an active research topic for some conditions. It will be our main problem in the case of air to aircraft heat transfer.
Approximations and conditions
h should be calculated from Computational fluid dynamics analysis, which requires a good expertise in the domain and complex software to be used. Since we don't have this capability, we explore existing approximations of the value. These approximations are only valid in some very specific conditions, each condition having a different approximation. Assumptions are also made, for example the temperature of the fluid and the body over the area of the heat transfer are assumed constant, as well as the flow rate. Approximation are often based on a fluid temperature equal to the arithmetic mean between the wall and the free stream. This is called the mean film temperature.
The Nusselt number Nu
The Nusselt number Nu is introduced when equating Newton's equation to the conduction heat:
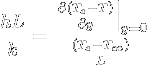 = Nu
= Nu
The Nusselt number is then the ratio of the temperature gradient at the surface to the reference temperature gradient, meaning that its value indicates the shape of the temperature gradient.
The Prandtl number Pr
The Prandtl number depends only on the fluid and its state, not on a characteristic length.
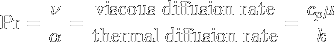
The Prandtl number controls the relative thickness of the momentum and thermal boundary layers. When Pr is small, it means that the heat diffuses very quickly compared to the velocity (momentum). This means that for liquid metals the thickness of the thermal boundary layer is much bigger than the velocity boundary layer. See page 223 of [2] for other interpretations of the values.
The Reynolds number Re
The Reynolds number gives a measure of the ratio of inertial forces to viscous forces.
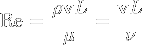
It is also useful because its value can indicate if the flow in the boundary layer is laminar (value < 350,000), turbulent (value > 500,000) or transitional between the two, in which case it depends on other factors such as surface roughness.
The Rayleigh number Ra
The Rayleigh number is an indicator for natural convection heat transfer. When it is below the critical value for a fluid, heat transfer is primarily in the form of conduction; when it exceeds the critical value, heat transfer is primarily in the form of convection.
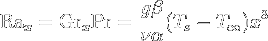
α is the thermal diffusivity  ; β is the thermal expansion coefficient, for an isobaric process it can be approximated to β = 1/T. x is the distance from the leading edge.
; β is the thermal expansion coefficient, for an isobaric process it can be approximated to β = 1/T. x is the distance from the leading edge.
Cases of application
We currently use heat transfer to estimate the rate of vaporization of cryogenic propellant on the ground and during the ascent to rocket ignition altitude. The latter could however be easily used to calculate the drag force of the aircraft fuselage on its tank part. In both case we can assume the fluids are incompressible and steady and that the temperatures are constant over the body and in the free stream fluid for a given altitude. The program using the atmospheric model and the flight path model to compute the heat transfer during flight is available freely here: File:Heat transfer to rocket tank.c.
Warning: the values presented below are highly dependent on the dimensions of the considered tank (diameter: 0.27m, length: 1.63m, surface: 1.38261m^2), which was given by the first approximation of the rocket mass program, the climb rates and flight profile (currently based on U-2's rate), and the temperature of the propellant (here LOX at 92K).
Warning: the method and results presented here are based on approximations and assumptions, and it may even have not been done in the proper way. Please validate the method used if you have some knowledge on convective heat transfer.
Natural convection for horizontal cryogenic tank
On the ground, the cryogenic propellant tank undergoes a large temperature difference and since it doesn't move it's the natural convection that is at work, if the wind is neglected. An approximation exists for the Nusselt number in this condition: horizontal cylinder in external flow under natural convection.
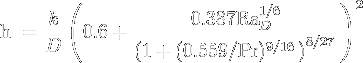
D is the diameter of the approximated cylinder, in our case we take 0.27m, given by a first evaluation of the rocket mass program.
Air density is derived from the atmospheric model at sea level, corrected to the actual ground temperature. For a 25°C or 298.15 K ground temperature:
- the density (rho) is 1.18391 kg/m^3
and at the mean film temperature of -78.07°C or 195.075 K, given the propellant and tank temperature of 92 K:
- the viscosity µ is 1.30015e-05 Pa.s (calculated using Sutherland's law)
- the kinematic viscosity nu is µ / rho = 1.0982e-5 m^2/s
- the specific heat Cp is 1007.68 J/kg.K (approximated using this interpolation)
- the Prandtl number is 0.73862
- the thermal conductivity of air k is 0.0177375 W/m.K (approximated using this interpolation)
- α is thus k/(rho.Cp) = 1.4868e-5 m^2/s
- β is approximated to 1/T = 1/195.075 = 5.126e-3 1/K
- RaD is ((9.80665 * 5.126e-3) / (1.0982e-5 * 1.4868e-5)) * (298.15 - 92) * 0.27^3 = 6.3467e10 * 0.27^3 = 1.24931e+9.
- finally, h is 0.0177375/0.27 * (0.6 + (0.387 * 1.24931e+9^1/6) / (1 + (0.559/0.73862)^9/16)^8/27)^2 = 8.20533 W/m^2.K
We finally have a heat transfer coefficient for air. We can compute the total heat transferred from it, using Newton's law equation (top). We need to specify the area on which the heat transfer will apply, the approximated cylinder, and the number of seconds during which the heat is transferred. Tanks are a cylinder with two hemispherical end-caps. Since the end-caps still conduct heat, we will include their area and assume it is part of the approximed cylinder's area. Assumed area is then 1.3826m^2. Let's take 600 seconds (10 minutes) for the time spent on the ground between tanks filling and aircraft lift-off. We assume the temperature to be constant on the ground and in the tank while heat is transferred. This is correct since the heat energy feeds a phase change in the propellant (vaporization) and not a temperature increase of some sort.
dQ/dt = h * A * (Tground - Tprop) = 8.20533 * 1.3826 * (298.15 - 92) = 2338.73 J/s.
We can now calculate the evaporation rate of the propellant with and without insulation. The heat of vaporization for LOX is 213 kJ/kg.
Without insulation, the vaporization rate of LOX is 11g/s, making 6.59kg of LOX evaporated in 600s.
With a 10mm Aerogel insulation, the thermal conductivity being 15 mW/m.K, its U-value being k/L = 0.015/0.010 = 1.5 W/m^2.K, the vaporization rate is 919.5mg/s. For 10 minutes, it goes down to 0.552kg (instead of 6.59 without insulation). The overall heat transfer coefficient U was calculated using this method.
Forced convection on aircraft fuselage during flight
Section 5.8 in [2], Heat transfer in turbulent flow over a flat plate, is the closest known answer to this problem. The tank's cylinder can be considered as a flat plate since there is no pressure change in the local y direction. The Colburn analogy is the approximation that applies in this case. It states that the local Nusselt number, assuming constant wall temperature, is Nux = 0.0292 Rex4/5 Pr1/3. This equation is however only valid for Rec < Rex < 107 and 0.7 < Pr < 100.
From what we calculated with the ISA model, Pr varies between 0.73 and 0.75, and the Reynolds number for the characteristic length L of the tank (ReL) drops from 4.36714e+07 to 6.68455e+06 with altitude. This value of Re confirms that the boundary layer is turbulent. [2] indicates that the Colburn analogy can still be used for Pr up to 10^8, but with some loss of accuracy. We use the following approximation to calculate the average Nusselt number for forced convection in turbulent flows:
NuL = 0.0366 (ReL0.8 - 14500) Pr1/3 given in [2].
The calculated average Nusselt number for ascent operation is 42353 at sea level and drops to 1037 at 30km altitude. hL can then be calculated too, hL = NuL * kair / L. It varies from 460.8 on the ground to 9.6 W/m^2.K at 30km altitude.
The simple flight path approximation is used to calculate the average h value for every second of the flight. We also need to calculate the dQ/dt value for each second, since the external temperature changes as the aircraft ascends. The integrated value of heat Q is finally: Q = 1710.94 kJ. For LOX, it translates into more than 80kg of oxidizer evaporated during the ascent, when no insulation is used. With an Aerogel insulation layer of 10mm, the mass of evaporated LOX is evaluated to 0.666kg. That corresponds to Q = 141.89 kJ. The overall heat transfer coefficient U was calculated using this method.
References
1. Principles of Heat Transfer: SI Edition, Frank Kreith, Raj M. Manglik, Mark S. Bohn, 2010. Google books
2. Textbook Of Heat Transfer (4th Edition), S.P. Sukhatme, 2006. Google books
3. Lecture on Advanced Heat Transfer, Ibrahim Sezai, 2011. Distributed as open courseware, here
A nice wiki page on heat transfer for rocket engines, regenerative cooling in particular: here.