Heat transfer

Heat transfer is a very complicated process involving many parameters and conditions. This page plays the role of introduction to heat transfer and a documentation on the methods used to calculate the heat transfers applied to our vehicle.

Heat transfers

A heat transfer is basically an energy transfer that can produce work or a change of temperature difference between the interacting parts. It can take three forms: conductive, convective and radiative. In the case of a heat transfer due to the atmosphere around an aircraft, the three mechanisms are effective. This page currently focuses on convective heat transfer, which implies conductive heat transfer. Radiative transfer is probably negligible before the two others in our particular case study.

Introduction to heat convection and conduction

Heat convection occurs when there is a fluid flowing around a control volume at a temperature different than the control volume's. The flow can be either natural, when the fluid is flowing due to density gradients (buoyancy force), or forced, when the fluid is flowing because an external process force it to flow or make the control volume move through the fluid.

When air is the considered fluid, convection is always associated to conduction heat transfer. The reason is that a film is formed on the surface of the object, called the boundary layer, and it is partly steady and at a temperature closer than the temperature of the object than the temperature of the fluid. In that case, conduction applies.

An insulation layer's effect can be easily calculated as its thermal transmittance (U-value) or resistance (R-value), the amount of heat that it allows to be transferred through it. This is directly obtained from the material's thermal conductivity k (unit: W/m.K) and the thickness of the insulation L. R = L/k and U = k/L. Unit of U is W/m^2.K. The transmitter heat is then Φ = A × U × (T1 - T2), in Watt (= Joule/s), where A is the external area of the insulation layer, T1 and T2 are the internal and external temperature. Examples for the transmittance of insulation layers can be found here [1],

Heat transfer coefficient h

The rate of heat loss of a body by convection is proportional to the difference in temperatures between the body and its surroundings, as stated by Newton's law of cooling: 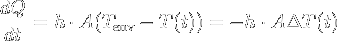, where h is the heat transfer coefficient. This h depends on many parameters (flow rate, surface roughness, fluid properties, and others) and is very hard to calculate accurately. Approximations exist for some conditions and determining them is still an active research topic for some conditions. It will be our main problem in the case of air to aircraft heat transfer.

Approximations and conditions

h should be calculated from Computational fluid dynamics analysis, which requires a good expertise in the domain and complex software to be used. Since we don't have this capability, we explore existing approximations of the value. These approximations are only valid in some very specific conditions, each condition having a different approximation. Assumptions are also made, for example the temperature of the fluid and the body over the area of the heat transfer are assumed constant, as well as the flow rate. Approximation are often based on a fluid temperature equal to the arithmetic mean between the wall and the free stream. This is called the mean film temperature.

The Nusselt number Nu

The Nusselt number Nu is introduced when equating Newton's equation to the conduction heat: 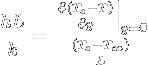= Nu.

The Nusselt number is then the ratio of the temperature gradient at the surface to the reference temperature gradient, meaning that its value indicates the shape of the temperature gradient.

Cases of application

We currently use heat transfer to estimate the rate of vaporization of the cryogenic propellants on the ground and during ascent to rocket ignition altitude. The latter could however be easily used to calculate the drag force of the aircraft fuselage on its tank part.

Natural convection for horizontal cryogenic tank

On the ground, the cryogenic propellant tank undergoes a large temperature difference and since it doesn't move it's the natural convection that is at work, if the wind is neglected. An approximation exists for the Nusselt number in this condition: horizontal cylinder in external flow under natural convection.

Air density is derived from the atmospheric model at sea level, corrected to the actual ground temperature. For a 25°C temperature, the density (rho) is 1.18391, and at the mean film temperature of -78.07°C, the viscosity µ is 1.30015e-05 Pa.s, the specific heat Cp is 1007.68 J/kg.K and the Prusselt number is 0.874462.

References

Principles of Heat Transfer: SI Edition, Frank Kreith, Raj M. Manglik, Mark S. Bohn, 2010. Google books

Textbook Of Heat Transfer (4th Edition), S.P. Sukhatme, 2006. Google books