Aero formulas: Difference between revisions
From NPrize
Jump to navigationJump to search
density |
m →Resources on physics related to aerodynamics: heat transfer link |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
The [https://en.wikipedia.org/wiki/List_of_elementary_physics_formulae List of elementary physics formulae] on wikipedia is useful. | The [https://en.wikipedia.org/wiki/List_of_elementary_physics_formulae List of elementary physics formulae] on wikipedia is useful. | ||
A page is dedicated to [[heat transfer]]. | |||
==List of variables== | ==List of variables== | ||
| Line 81: | Line 83: | ||
| Pressure. p<sub>t</sub> is the [https://en.wikipedia.org/wiki/Stagnation_pressure stagnation pressure]. | | Pressure. p<sub>t</sub> is the [https://en.wikipedia.org/wiki/Stagnation_pressure stagnation pressure]. | ||
| Pa (Pascal) | | Pa (Pascal) | ||
|- | |||
| p | |||
| [https://en.wikipedia.org/wiki/Momentum Momentum] p = m*v, with m the mass and v the velocity, not to be confused with volume. | |||
| kg.m.s<sup>-1</sup> | |||
|} | |} | ||
| Line 100: | Line 106: | ||
| 8.3144621 | | 8.3144621 | ||
| J.K<sup>−1</sup>.mol<sup>−1</sup> | | J.K<sup>−1</sup>.mol<sup>−1</sup> | ||
|- | |||
| G | |||
| [https://en.wikipedia.org/wiki/Gravitational_constant Gravitational constant] | |||
| 6.674 | |||
| m<sup>3</sup>.kg<sup>-1</sup>.s<sup>-2</sup> | |||
|- | |- | ||
| k<sub>B</sub> or k | | k<sub>B</sub> or k | ||
| Line 114: | Line 125: | ||
!Meaning | !Meaning | ||
|- | |- | ||
|{{SERVER}}/images/formulas_mirror/pvnrtk_neg.png | |||
|Ideal gas equation | |Ideal gas equation | ||
|Relation between properties of an ideal gas ([https://en.wikipedia.org/wiki/State_equation state equation]). k is k<sub>B</sub>. | |Relation between properties of an ideal gas ([https://en.wikipedia.org/wiki/State_equation state equation]). k is k<sub>B</sub>. | ||
|- | |- | ||
|{{SERVER}}/images/formulas_mirror/clausius-clapeyron_neg.png | |||
|[https://en.wikipedia.org/wiki/Clausius%E2%80%93Clapeyron_relation#Ideal_gas_approximation_at_low_temperatures Clausius-Clapeyron relation] | |[https://en.wikipedia.org/wiki/Clausius%E2%80%93Clapeyron_relation#Ideal_gas_approximation_at_low_temperatures Clausius-Clapeyron relation] | ||
|Relation between the pressure, latent heat of vaporization and temperature of a vapour at two temperatures (approximation, at low temperatures). | |Relation between the pressure, latent heat of vaporization and temperature of a vapour at two temperatures (approximation, at low temperatures). | ||
|- | |- | ||
|{{SERVER}}/images/formulas_mirror/QeqmL_neg.png | |||
|Heat at [https://en.wikipedia.org/wiki/Latent_heat#Specific_latent_heat state change] for an ideal gas. | |Heat at [https://en.wikipedia.org/wiki/Latent_heat#Specific_latent_heat state change] for an ideal gas. | ||
|The heat required to change the state of a some matter, L being the latent heat. Delta H equals Q only when pressure is constant (isobaric). | |The heat required to change the state of a some matter, L being the latent heat. Delta H equals Q only when pressure is constant (isobaric). | ||
|- | |- | ||
|{{SERVER}}/images/formulas_mirror/dUeqdQmindW_neg.png | |||
|[https://en.wikipedia.org/wiki/First_law_of_thermodynamics First law of thermodynamics] | |[https://en.wikipedia.org/wiki/First_law_of_thermodynamics First law of thermodynamics] | ||
|Variations of internal energy of a system between two states is the sum of the received heat and work (minus the ''given'' work). | |Variations of internal energy of a system between two states is the sum of the received heat and work (minus the ''given'' work). | ||
|- | |- | ||
|{{SERVER}}/images/formulas_mirror/enthalpy_neg.png | |||
|[https://en.wikipedia.org/wiki/Enthalpy Enthalpy] | |[https://en.wikipedia.org/wiki/Enthalpy Enthalpy] | ||
|Total amount of energy of a system, defined as the sum of the internal energy U of the system and pressure * volume at the boundary of the system and its environment. | |Total amount of energy of a system, defined as the sum of the internal energy U of the system and pressure * volume at the boundary of the system and its environment. | ||
|- | |- | ||
|{{SERVER}}/images/formulas_mirror/workExpand_neg.png | |||
|Work of gas expansion. | |Work of gas expansion. | ||
|Work done by expanding an ideal gas. | |Work done by expanding an ideal gas. | ||
|- | |- | ||
|{{SERVER}}/images/formulas_mirror/entropy_dueqtdsmpdv_neg.png | |||
|[https://en.wikipedia.org/wiki/Entropy | |[https://en.wikipedia.org/wiki/Internal_energy Internal energy] change related to [https://en.wikipedia.org/wiki/Entropy entropy] | ||
|Internal energy related to entropy variation for a closed system in thermal equilibrium ([https://en.wikipedia.org/wiki/Fundamental_thermodynamic_relation fundamental thermodynamic relation]). | |Internal energy related to entropy variation for a closed system in thermal equilibrium ([https://en.wikipedia.org/wiki/Fundamental_thermodynamic_relation fundamental thermodynamic relation]). | ||
|- | |||
|{{SERVER}}/images/formulas_mirror/dheqtds_neg.png | |||
|[https://en.wikipedia.org/wiki/Enthalpy Enthalpy] change | |||
|Enthalpy change depending on entropy and pressure changes, equation created from the mix of the basic ones above. | |||
|- | |- | ||
|ΔS<sub>universe</sub> = ΔS<sub>surroundings</sub> + ΔS<sub>system</sub> | |ΔS<sub>universe</sub> = ΔS<sub>surroundings</sub> + ΔS<sub>system</sub> | ||
| Line 146: | Line 161: | ||
|Entropy variation of a system is generally compensated by the inverse variation of the surroundings, not including losses. | |Entropy variation of a system is generally compensated by the inverse variation of the surroundings, not including losses. | ||
|- | |- | ||
|{{SERVER}}/images/formulas_mirror/dS_neg.png | |||
|[https://en.wikipedia.org/wiki/Second_law_of_thermodynamics Second law of thermodynamics] | |[https://en.wikipedia.org/wiki/Second_law_of_thermodynamics Second law of thermodynamics] | ||
|A change in the entropy of a system is the infinitesimal transfer of heat to a closed system driving a reversible process, divided by the equilibrium temperature of the system. | |A change in the entropy of a system is the infinitesimal transfer of heat to a closed system driving a reversible process, divided by the equilibrium temperature of the system. | ||
|- | |- | ||
|{{SERVER}}/images/formulas_mirror/gibbs_neg.png | |||
|[https://en.wikipedia.org/wiki/Gibbs_free_energy Gibbs free energy] / Free enthalpy | |[https://en.wikipedia.org/wiki/Gibbs_free_energy Gibbs free energy] / Free enthalpy | ||
|Useful work obtainable from a system at '''isobaric''' and '''isothermal''' conditions. Since H is U + pV, it can be replaced in the equation, making G = H - TS. | |Useful work obtainable from a system at '''isobaric''' and '''isothermal''' conditions. Since H is U + pV, it can be replaced in the equation, making G = H - TS. | ||
|- | |- | ||
|{{SERVER}}/images/formulas_mirror/deltaG_neg.png | |||
|[https://en.wikipedia.org/wiki/Gibbs_free_energy Gibbs free energy] variation. | |[https://en.wikipedia.org/wiki/Gibbs_free_energy Gibbs free energy] variation. | ||
|If ΔG < 0, the system's transformation can be spontaneous, if ΔG = 0 the transformation is inversible and the system is in an equilibrium state, if ΔG > 0 it can't be spontaneous. | |If ΔG < 0, the system's transformation can be spontaneous, if ΔG = 0 the transformation is inversible and the system is in an equilibrium state, if ΔG > 0 it can't be spontaneous. | ||
|- | |- | ||
|{{SERVER}}/images/formulas_mirror/density_ideal_neg.png | |||
|[https://en.wikipedia.org/wiki/Density#Changes_of_density Density] of an ideal gas. | |[https://en.wikipedia.org/wiki/Density#Changes_of_density Density] of an ideal gas. | ||
|M is molar mass. This means that the density of an ideal gas can be doubled by doubling the pressure, or by halving the absolute temperature. | |M is molar mass. This means that the density of an ideal gas can be doubled by doubling the pressure, or by halving the absolute temperature. | ||
|} | |} | ||
Latest revision as of 22:42, 20 November 2012
The List of elementary physics formulae on wikipedia is useful.
A page is dedicated to heat transfer.
List of variables
| Variable | Meaning | Unit (SI) |
|---|---|---|
| γ (gamma) | Surface tension or Heat capacity ratio (adiabatic process in thermodynamics) | N.m-1 (Newton per meter) |
| μ (mu) or η (eta) | Viscosity | Pa·s (Pascal second) or P (Poise, 1 Poise is 0.1 Pa.s) |
| ρ (rho) | Density | kg.m-3 (kg per cubic meter) |
| C, Cp, CV | Heat capacity, general, at constant pressure, at constant volume. | J.K-1 (Joule per Kelvin) |
| G | Gibbs free energy | J (Joule) |
| H | Enthalpy: total energy of a thermodynamic system. | J (Joule) |
| ΔHvap or L | Vaporization heat or Latent heat of vaporization: energy required to vaporize a mole of liquid at a given temperature. | J.mol-1 (Joule per mole) |
| M | Mach number | no unit |
| Q | Amount of Heat | J (Joule) |
| T | Temperature. T0 or Tt is the stagnation temperature. | K (Kelvin) |
| S | Entropy | J.K-1 (Joule per Kelvin) |
| U | Internal energy of a system (see first law of Thermodynamics below) | J (Joule) |
| V | Volume | m3 (cubic meter) |
| W | Work: mechanical constraints on the system. | J (Joule) |
| a | Speed of sound in medium (used to calculate Mach number) | m.s-1 |
| c | Velocity of a flow in thermodynamics, also noted V; generally noted u in fluid dynamics. | m.s-1 |
| n | Quantity of matter | mol (mole) |
| p | Pressure. pt is the stagnation pressure. | Pa (Pascal) |
| p | Momentum p = m*v, with m the mass and v the velocity, not to be confused with volume. | kg.m.s-1 |
List of constants
| Constant | Meaning | Value | Unit (SI) |
|---|---|---|---|
| NA or N | Avogadro constant, number of atoms or molecules in a mole. | 6.02214129.1023 | mol-1 |
| R | ideal gas constant | 8.3144621 | J.K−1.mol−1 |
| G | Gravitational constant | 6.674 | m3.kg-1.s-2 |
| kB or k | Boltzmann constant, gas constant R divided by Avogadro number. | 1.3806488.10-23 | J.K-1 |
List of equations
| Equation | Name | Meaning |
|---|---|---|
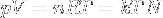
|
Ideal gas equation | Relation between properties of an ideal gas (state equation). k is kB. |
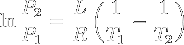
|
Clausius-Clapeyron relation | Relation between the pressure, latent heat of vaporization and temperature of a vapour at two temperatures (approximation, at low temperatures). |
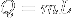
|
Heat at state change for an ideal gas. | The heat required to change the state of a some matter, L being the latent heat. Delta H equals Q only when pressure is constant (isobaric). |
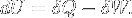
|
First law of thermodynamics | Variations of internal energy of a system between two states is the sum of the received heat and work (minus the given work). |
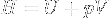
|
Enthalpy | Total amount of energy of a system, defined as the sum of the internal energy U of the system and pressure * volume at the boundary of the system and its environment. |
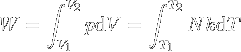
|
Work of gas expansion. | Work done by expanding an ideal gas. |
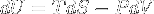
|
Internal energy change related to entropy | Internal energy related to entropy variation for a closed system in thermal equilibrium (fundamental thermodynamic relation). |
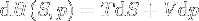
|
Enthalpy change | Enthalpy change depending on entropy and pressure changes, equation created from the mix of the basic ones above. |
| ΔSuniverse = ΔSsurroundings + ΔSsystem | Entropy variation as a whole. | Entropy variation of a system is generally compensated by the inverse variation of the surroundings, not including losses. |
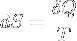
|
Second law of thermodynamics | A change in the entropy of a system is the infinitesimal transfer of heat to a closed system driving a reversible process, divided by the equilibrium temperature of the system. |
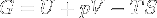
|
Gibbs free energy / Free enthalpy | Useful work obtainable from a system at isobaric and isothermal conditions. Since H is U + pV, it can be replaced in the equation, making G = H - TS. |
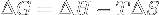
|
Gibbs free energy variation. | If ΔG < 0, the system's transformation can be spontaneous, if ΔG = 0 the transformation is inversible and the system is in an equilibrium state, if ΔG > 0 it can't be spontaneous. |
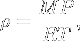
|
Density of an ideal gas. | M is molar mass. This means that the density of an ideal gas can be doubled by doubling the pressure, or by halving the absolute temperature. |