Rocket:First approximations

First approximations for our rocket

This page summarizes the important points about rockets launched from balloon or from aircraft, mainly what minimum mass we can expect. This information is used as a first approximation for the design of other systems, like the aircraft and its engines. Information about particular systems of rocket engines can be found in the rocket engines page.

Delta V requirements

The delta V we will require to achieve orbit depends on several factors:

• rocket launch altitude, the higher it is, the less delta V is required to face atmospheric drag and climb against gravity (gravity drag) and actually start the useful horizontal delta V. The planned release altitude is 30km ±5km, so that leaves at least 100km to climb, probably even 160km if we want to be able to do 9 orbits, because of aerodynamic drag on upper atmosphere with such a small satellite.
• rocket launch velocity, which is close to the velocity of the aircraft at rocket release. If the aircraft can do its release with the same velocity vector than the rocket flight path's beginning, this speed will be completely used by the rocket; if the aircraft needs to release the rocket and then after a few seconds the rocket fires, the z component of the velocity vector is probably lost.
• high-altitude flight strategy, a choice that has to be made between subsonic flight with large wingspan and reduced thrust or supersonic flight with high power engines.
  • Choice 1 (subsonic) has a planned horizontal release velocity of 270m/s ±20m/s (0.9M) and a quite small, 5° ± 5° vertical release velocity.
  • Choice 2 (supersonic) has a planned horizontal release velocity still unknown, possibly 1.5M ±0.5M but has the advantage of giving a higher release altitude and vertical velocity component, likely consistent with the rocket flight path initial vector.
• launch latitude, important for ground launches, the latitude determines the speed given by Earth's rotation. We have to keep in mind that the aircraft velocity is relative to the centre of the Earth and not to the surface.
• final velocity of the rocket, which is the same than the satellite velocity, it is the main part of the delta V. At an altitude of 200km, the orbital speed is 7.8 km/s, and it doesn't change much for an altitude ±100km.

Delta V achievement

Once we have a realistic estimation of the required delta V for our rocket, we can start thinking about the characteristics of the rocket by itself and of its engine.

The rocket equation tells us that 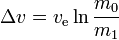, where m₀ is the initial total mass including propellant, m₁ is the final total mass (dry rocket mass), and v_e is the effective exhaust velocity. The given delta v doesn't take into account gravity and other forces acting on the vehicle.

• the exhaust velocity of rocket engine's produced gas is closely related to the Isp of the engine, as we can see here: 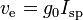. For the duet LOX/E85 we chose, max Isp should be between the max Isp of RP-1 (353s) and max Isp of 92.5% alcohol (338s), so around 344 ± 6s. Isp is very important and we should aim and actual Isp approaching 20s from the max Isp. Max Isp is vacuum Isp with the most efficient rocket engine, the sea level Isp is generally around 10% less, and since we will use a cheap design, we may not have the optimal nozzle.

• thrust is related to this exhaust velocity in the following way 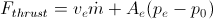. It is not directly related to the delta v, but it is related to the mass of the payload that has to be accelerated. Ion engines provide very high Isp and v_e but they don't provide enough thrust so they can be used to launch something from Earth to space.

• the dry mass of the rocket, once the fuel and consequently Isp have been fixed, is the most important factor. The lighter the rocket, the more efficient it will be in term of delta V. To make a light rocket, high quality materials, thus expensive, must be used. What takes the most volume in a rocket is the fuel and oxidizer tanks. If tanks are solid enough, and this may be a requirements depending on what they contain, they can be used as part of the structure of the rocket. If they are not solid, a external skeleton has to be build that will undergo all mechanical forces that apply to the vehicle. For the N-prize, the payload mass is nearly insignificant compared to the rocket mass, which is good for the delta V.

• the mass of the engine itself is closely related to the type fuel delivery system used (what kind of pump or tank pressurization) and to the thrust it produces. The trust to mass ratio depends mostly on chamber pressure, which depends on the capabilities of the fuel pumps system and the efficiency of the regenerative cooling of the chamber and nozzle.

As an example, if the delta V is 9.0km/s, and that we have a 340s Isp, the required mass ratio of propellant is 1-e^(-9.0/3.3) = 93.4%, which may be close to impossible. With a 8.0km/s delta V, assuming we have a higher release velocity, the same rocket engine and still only one rocket stage, it becomes 91.1%, still very hard. A two stage rocket can do this, see the examples in the rocket equation Wikipedia page, but if we need to build two rocket engines' systems, we can be sure that we will exceed the money requirement.

So the main question becomes: on what subsystems can we found cheap alternatives to decrease the mass of the rocket?