Rocket:First approximations

First approximations for our rocket

This page summarizes the important numbers about rockets launched from balloon or from aircraft, mainly what minimum vehicle mass we can expect. The two first sections about Delta V, combined with the famous rocket equation, serve as basis to evaluate the mass ratio of the rocket. More study is required to derive a minimum mass estimation from this, done in following secitons. This information is used as a first approximation for the design of other systems, like the aircraft and its engines. Information about particular systems of rocket engines can be found in the rocket engines page.

Delta V requirements

The delta V we will require to achieve orbit depends on several factors:

• rocket launch altitude, the higher it is, the less delta V is required to face atmospheric drag and climb against gravity (gravity drag) and actually start the useful horizontal delta V. The planned release altitude is 30km ±5km, so that leaves at least 100km to climb, probably even 160km if we want to be able to do 9 orbits, because of aerodynamic drag on upper atmosphere for such a small satellite.
  • Atmospheric drag should be very low at this altitude, although it scales badly with small vehicles as explained at many places, in particular in this paper . The paper also models the delta V losses and states that the difference between ground launch and a subsonic 40'000 ft (12km) launch is 1.5km/s, for a 77kg/20cm diameter vehicle, which is huge! (see page 46). It still has to be calculated in our conditions. If we need to pitch up after rocket release this drag will increase.
  • Gravity drag is about 1100m/s to 1500m/s with ground launch, and it is said here that Orbital's Pegasus system has its delta V reduced by approximately 750m/s with the aircraft cruise launch (40'000 feet, 500mph).
• rocket launch velocity, which is close to the velocity of the aircraft at rocket release. If the aircraft can do its release with the same velocity vector than the rocket flight path's beginning, this speed will be completely used by the rocket; if the aircraft needs to release the rocket and then after a few seconds the rocket fires, the z component of the velocity vector is probably lost.
• high-altitude flight strategy, a choice that has to be made between subsonic flight with large wingspan and reduced thrust or supersonic flight with high power engines.
  • Choice 1 (subsonic) has a planned horizontal release velocity of 270m/s ±20m/s (0.9M) and a quite small, 5° ± 5° vertical release velocity.
  • Choice 2 (supersonic) has a planned horizontal release velocity still unknown, possibly 1.5M ±0.5M but has the advantage of giving a higher release altitude and vertical velocity component, likely consistent with the rocket flight path initial vector.
• launch latitude, important for ground launches, the latitude determines the speed given by Earth's rotation. We have to keep in mind that the aircraft velocity is relative to the centre of the Earth and not to the surface. We don't know where we will be able to launch it yet, so let's take a conservative value for now, 300m/s. At equator, it is 465m/s.
• final velocity of the rocket, which is probably the same than the satellite velocity, except if we decide to catapult it from the rocket somehow, it is the main part of the delta V. At an altitude of 200km, the orbital speed is 7.8 km/s, and it doesn't change much for an altitude ±100km.

Our delta V will then be (if numbers are not explained above, they are just guessed until they are correct):

• For choice 1: 7800 (orbital speed) + 70 (atmospheric loss) + 700 (gravity loss) - 270 (release velocity) - 300 (earth rotation) = 8000m/s
• For choice 2: 7800 (orbital speed) + 100 (atmospheric loss) + 550 (gravity loss) - 400 (release velocity) - 300 (earth rotation) = 7750m/s

Delta V achievement

Once we have a realistic estimation of the required delta V for our rocket, we can start thinking about the characteristics of the rocket by itself and of its engine.

The rocket equation tells us that 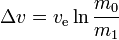, where m₀ is the initial total mass including propellant, m₁ is the final total mass (dry rocket mass), and v_e is the effective exhaust velocity. The given delta V doesn't take into account gravity and other forces acting on the vehicle.

• the exhaust velocity of rocket engine's produced gas is closely related to the Isp of the engine, as we can see here: 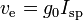. For the duet LOX/E85 we chose, max Isp should be between the max Isp of RP-1 (353s) and max Isp of 92.5% alcohol (338s), so around 344 ± 6s. Isp is very important and we should aim and actual Isp approaching 20s from the max Isp. Max Isp is vacuum Isp with the most efficient rocket engine, the sea level Isp is generally around 10% less, and since we will use a cheap design, we may not have the optimal nozzle and fuel combustion efficiency.
• thrust is related to this exhaust velocity in the following way 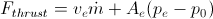. It is not directly related to the delta V, but it is related to the mass of the payload that has to be accelerated. For example, Ion engines provide very high Isp and v_e but they don't provide enough thrust so they can be used to launch something from Earth to space.
• the dry mass of the rocket, once the fuel and consequently Isp have been fixed, is the most important factor. The lighter the rocket compared to the fuel, the more efficient it will be in term of delta V. As the mass ratio will be fixed by the rocket equation, it also means that the lighter the rocket, the many times less fuel will be required and the smaller the rocket. To make a light rocket, high quality materials, thus expensive, should be used. This is studied in the next section. For the N-prize, the payload mass is nearly insignificant compared to the rocket mass, which is good for the delta V.
  • the mass of the engine itself is closely related to the type fuel delivery system used (what kind of pump or tank pressurization) and to the thrust it produces. The thrust-to-weight ratio depends mostly on chamber pressure, which depends on the capabilities of the fuel pumps system and the efficiency of the regenerative cooling of the chamber and nozzle. Also studied below.

As an example, if the delta V is 9.0km/s, and that we have a 340s Isp, the required mass ratio of propellant is 1-e^(-9.0/3.3) = 93.4%, which is very hard to achieve. SpaceX has done it better than 95% (see spacefellowship forum thread on SSTO) for a first stage, so it doesn't include the payload, fairing, and so on. The Haas 2c rocket from ARCA (Romania) is also very lightweight and aims to be an SSTO demonstrator. Their engine has an very nice 110:1 thrust-to-mass ratio, the rocket having a 96.9% mass of fuel. The engine supports only 3 minutes of operation, will it be enough to reach orbital speed?

With a 8.0km/s delta V, assuming we have a higher release velocity, the same rocket engine and still only one rocket stage, it becomes 91.1%, still quite hard. A two stage rocket can do this, see the examples in the rocket equation Wikipedia page, but if we need to build two rocket engines' systems, we can be sure that we will exceed the money requirement.

So the main question becomes: on what subsystems can we found cheap alternatives to decrease the mass of the rocket?

Systems design for minimum mass

The mass ratio evaluated above does not tell us what mass we should expect from the rocket. It depends on the minimum mass all systems can be integrated: engine, tanks, structure, avionics, communications and other controls. The reference addresses this subject.

Rocket engine

Since we will design our own rocket engine to meet the cost requirement, we can design an engine for any thrust. We just have to fix a thrust-to-weight ratio for the engine, so that we can fix it when the rest of the vehicle's mass is evaluated. The thrust-to-weight ratio for the entire rocket will also be required, as it will determine what will be the initial acceleration. To avoid atmospheric drag losses and minimize gravity drag losses, and from what we could find in the literature , a ratio of 2.0 is common for small vehicles. Another source states the opposite, that since we're not launching in vertical direction, we don't need as much ratio, and 1.25 is enough. It is, if losses are not taken into account.

The thrust-to-weight ratio for the engine doesn't scale linearly either, but in our advantage here . A ratio of more than 100 is common in small launchers' engines .

Fuel tanks

Fuel tanks mass depend mostly on the type of fuel delivery system used: pressurization or pumping. When using pressurized tanks to force the fuel into the engine, the tanks have to sustain the pressure and must have thicker walls. A pumped fuel only requires the fuel to not leak into vacuum, since we are going to space. For kerosene-like fuel, it can be very simple. For the cryogenic oxidizer, it's more complicated due to the evaporation losses related to poor isolation and to metal weakening with large temperature differential.

Structure

What takes the most volume in a rocket is the fuel and oxidizer tanks. If tanks are solid enough, they can be used as part of the structure of the rocket. If they are not solid, a external skeleton has to be build that will undergo all mechanical forces that apply to the vehicle. The max Q, maximum dynamic pressure that the vehicle has to withstand, is reduced when launching from altitude than from ground, so the structure may slightly get lighter.

Avionics

estimated in 1999 that avionics could fit in 50g and 220g for batteries, but it used differential thrust throttling on several engines instead of gimbals or RCS.

Other elements

GIMBAL, Valves, pressurization system, RCS, communication, fairing, separation system at least.