Aero formulas: Difference between revisions
From NPrize
Jump to navigationJump to search
more entropy and variables |
more thermodynamics |
||
| Line 111: | Line 111: | ||
|- | |- | ||
|style="background:white"| {{SERVER}}/images/formulas_mirror/dUeqdQmindW.png | |style="background:white"| {{SERVER}}/images/formulas_mirror/dUeqdQmindW.png | ||
|[https://en.wikipedia.org/wiki/First_law_of_thermodynamics First law of | |[https://en.wikipedia.org/wiki/First_law_of_thermodynamics First law of thermodynamics] | ||
|Variations of internal energy of a system between two states is the sum of the received heat and work (minus the ''given'' work). | |Variations of internal energy of a system between two states is the sum of the received heat and work (minus the ''given'' work). | ||
|- | |- | ||
|style="background:white"| {{SERVER}}/images/formulas_mirror/enthalpy.png | |style="background:white"| {{SERVER}}/images/formulas_mirror/enthalpy.png | ||
|[https://en.wikipedia.org/wiki/Enthalpy Enthalpy] | |[https://en.wikipedia.org/wiki/Enthalpy Enthalpy] | ||
|Total amount of energy of a system, defined as the sum of the internal energy U and pressure * volume. | |Total amount of energy of a system, defined as the sum of the internal energy U of the system and pressure * volume at the boundary of the system and its environment. | ||
|- | |- | ||
|style="background:white"| {{SERVER}}/images/formulas_mirror/workExpand.png | |style="background:white"| {{SERVER}}/images/formulas_mirror/workExpand.png | ||
| Line 129: | Line 129: | ||
|Entropy variation as a whole. | |Entropy variation as a whole. | ||
|Entropy variation of a system is generally compensated by the inverse variation of the surroundings, not including losses. | |Entropy variation of a system is generally compensated by the inverse variation of the surroundings, not including losses. | ||
|- | |||
|style="background:white"| {{SERVER}}/images/formulas_mirror/dS.png | |||
|[https://en.wikipedia.org/wiki/Second_law_of_thermodynamics Second law of thermodynamics] | |||
|A change in the entropy of a system is the infinitesimal transfer of heat to a closed system driving a reversible process, divided by the equilibrium temperature of the system. | |||
|- | |- | ||
|style="background:white"| {{SERVER}}/images/formulas_mirror/gibbs.png | |style="background:white"| {{SERVER}}/images/formulas_mirror/gibbs.png | ||
|[https://en.wikipedia.org/wiki/Gibbs_free_energy Gibbs free energy] / Free enthalpy | |[https://en.wikipedia.org/wiki/Gibbs_free_energy Gibbs free energy] / Free enthalpy | ||
|Useful work obtainable from a system at isobaric and isothermal conditions. Since H is U + pV, it can be replaced in the equation, making G = H - TS. | |Useful work obtainable from a system at '''isobaric''' and '''isothermal''' conditions. Since H is U + pV, it can be replaced in the equation, making G = H - TS. | ||
|- | |- | ||
|style="background:white"| {{SERVER}}/images/formulas_mirror/deltaG.png | |style="background:white"| {{SERVER}}/images/formulas_mirror/deltaG.png | ||
|[https://en.wikipedia.org/wiki/Gibbs_free_energy Gibbs free energy] variation. | |[https://en.wikipedia.org/wiki/Gibbs_free_energy Gibbs free energy] variation. | ||
| | |If ΔG < 0, the system's transformation can be spontaneous, if ΔG = 0 the transformation is inversible and the system is in an equilibrium state, if ΔG > 0 it can't be spontaneous. | ||
|} | |} | ||
Revision as of 00:25, 11 April 2012
The List of elementary physics formulae on wikipedia is useful.
List of variables
| Variable | Meaning | Unit (SI) |
|---|---|---|
| γ (gamma) | Surface tension | N.m-1 (Newton per meter) |
| μ (mu) or η (eta) | Viscosity | Pa·s (Pascal second) or P (Poise, 1 Poise is 0.1 Pa.s) |
| C, Cp, CV | Heat capacity, general, at constant pressure, at constant volume. | J.K-1 (Joule per Kelvin) |
| G | Gibbs free energy | J (Joule) |
| H | Enthalpy: total energy of a thermodynamic system. | J (Joule) |
| ΔHvap or L | Vaporization heat or Latent heat of vaporization: energy required to vaporize a mole of liquid at a given temperature. | J.mol-1 (Joule per mole) |
| Q | Amount of Heat | J (Joule) |
| T | Temperature | K (Kelvin) |
| S | Entropy | J.K-1 (Joule per Kelvin) |
| U | Internal energy of a system (see first law of Thermodynamics below) | J (Joule) |
| V | Volume | m3 (cubic meter) |
| W | Work: mechanical constraints on the system. | J (Joule) |
| n | Quantity of matter | mol (mole) |
| p | Pressure | Pa (Pascal) |
List of constants
| Constant | Meaning | Value | Unit (SI) |
|---|---|---|---|
| NA or N | Avogadro constant, number of atoms or molecules in a mole. | 6.02214129.1023 | mol-1 |
| R | ideal gas constant | 8.3144621 | J.K−1.mol−1 |
| kB or k | Boltzmann constant, gas constant R divided by Avogadro number. | 1.3806488.10-23 | J.K-1 |
List of equations
| Equation | Name | Meaning |
|---|---|---|
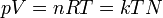
|
Ideal gas equation | Relation between properties of an ideal gas (state equation). k is kB. |
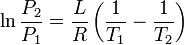
|
Clausius-Clapeyron relation | Relation between the pressure, latent heat of vaporization and temperature of a vapour at two temperatures (approximation, at low temperatures). |
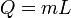
|
Heat at state change for an ideal gas. | The heat required to change the state of a some matter, L being the latent heat. Delta H equals Q only when pressure is constant (isobaric). |
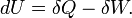
|
First law of thermodynamics | Variations of internal energy of a system between two states is the sum of the received heat and work (minus the given work). |
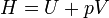
|
Enthalpy | Total amount of energy of a system, defined as the sum of the internal energy U of the system and pressure * volume at the boundary of the system and its environment. |
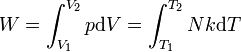
|
Work of gas expansion. | Work done by expanding an ideal gas. |
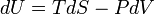
|
Entropy | Internal energy related to entropy variation for a closed system in thermal equilibrium (fundamental thermodynamic relation). |
| ΔSuniverse = ΔSsurroundings + ΔSsystem | Entropy variation as a whole. | Entropy variation of a system is generally compensated by the inverse variation of the surroundings, not including losses. |
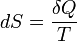
|
Second law of thermodynamics | A change in the entropy of a system is the infinitesimal transfer of heat to a closed system driving a reversible process, divided by the equilibrium temperature of the system. |
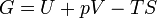
|
Gibbs free energy / Free enthalpy | Useful work obtainable from a system at isobaric and isothermal conditions. Since H is U + pV, it can be replaced in the equation, making G = H - TS. |
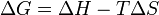
|
Gibbs free energy variation. | If ΔG < 0, the system's transformation can be spontaneous, if ΔG = 0 the transformation is inversible and the system is in an equilibrium state, if ΔG > 0 it can't be spontaneous. |