Rocket:First approximations
First approximations for our rocket
This page summarizes the important points about rockets launched from balloon or from aircraft, mainly what minimum mass we can expect. This information is used as a first approximation for the design of other systems, like the aircraft and its engines. Information about particular systems of rocket engines can be found in the rocket engines page.
Delta V requirements
The delta V we will require depends on several factors:
- rocket launch altitude, the higher it is, the less delta V is required to face atmospheric drag and to exit the atmosphere and actually start the useful horizontal delta V. The planned release altitude is 30km ±5km, so that leaves at least 100km to climb, probably even 170 if we want to be able to do 9 orbits, because of aerodynamic drag on upper atmosphere with such a small satellite.
- rocket launch speed, which is close to the speed of the aircraft at rocket release. If the aircraft can do its release with the same velocity vector than the rocket flight path's beginning, this speed will be completely used by the rocket; if the aircraft needs to release the rocket and then after a few seconds the rocket fires, the z component of the velocity vector is probably lost.
- high-altitude flight strategy, a choice that has to be made between subsonic flight with large wingspan and reduced thrust or supersonic flight with high power engines.
- Choice 1 has a planned horizontal release velocity of 270m/s ±20m/s (0.9M) and a quite small, 5° ± 5° vertical release velocity.
- Choice 2 has a planned horizontal release velocity still unknown, possibly 1.5M ±0.5M but has the advantage of giving a higher release altitude and vertical component, likely consistent with the rocket flight path initial vector.
- final velocity of the rocket, which is the same than the satellite velocity in our SSTO rocket case. At an altitude of 200km, the orbital speed is 7.8 km/s.
Delta V achievement
Once we have a realistic estimation of the required delta V for our rocket, we can start thinking about the characteristics of the rocket by itself and of its engine.
The rocket equation tells us that  , where m0 is the initial total mass including propellant, m1 is the final total mass (dry rocket mass), and ve is the effective exhaust velocity. The given delta v doesn't take into account gravity and other forces acting on the vehicle.
, where m0 is the initial total mass including propellant, m1 is the final total mass (dry rocket mass), and ve is the effective exhaust velocity. The given delta v doesn't take into account gravity and other forces acting on the vehicle.
- the exhaust velocity of rocket engine's produced gas is closely related to the Isp of the engine, as we can see here:
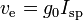 . For the duet LOX/E85 we chose, max Isp should be between the max Isp of RP-1 (353s) and max Isp of 92.5% alcohol (338s), so around 344 ± 6s. Isp is very important and we should aim and actual Isp approaching 20s from the max Isp. Max Isp is vacuum Isp with the best most efficient rocket engine,
. For the duet LOX/E85 we chose, max Isp should be between the max Isp of RP-1 (353s) and max Isp of 92.5% alcohol (338s), so around 344 ± 6s. Isp is very important and we should aim and actual Isp approaching 20s from the max Isp. Max Isp is vacuum Isp with the best most efficient rocket engine,
- thrust is related to this exhaust velocity in the following way
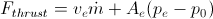 . It is not directly related to the delta v, but it is related to the mass of the payload that has to be accelerated. Ion engines provide very high Isp and ve but they don't provide enough thrust so they can be used to launch something from Earth to space.
. It is not directly related to the delta v, but it is related to the mass of the payload that has to be accelerated. Ion engines provide very high Isp and ve but they don't provide enough thrust so they can be used to launch something from Earth to space.
- the dry mass of the rocket, once the fuel and consequently Isp have been fixed, is the most important factor. The lighter the rocket, the more efficient it will be in term of delta V. To make a light rocket, high quality materials, thus expensive, must be used. What takes the most volume in a rocket is the fuel and oxidizer tanks. If tanks are solid enough, and this may be a requirements depending on what they contain, they can be used as part of the structure of the rocket. If they are not solid, a external skeleton has to be build that will undergo all mechanical forces that apply to the vehicle. For the N-prize, the payload mass is nearly insignificant compared to the rocket mass, which is good for the delta V.
- the mass of the engine itself is closely related to the type fuel delivery system used (what kind of pump or tank pressurization) and to the thrust it produces. The trust to mass ratio depends mostly on chamber pressure, which depends on the capabilities of the fuel pumps system and the efficiency of the regenerative cooling of the chamber and nozzle.